ISSN: 2007-7033 | Núm. 63 | e1664 | Sección abierta: artículos de investigación
Decisiones en reuniones de academia:
el caso de un profesor de matemáticas
Decisions in academy meetings:
the case of a mathematics professor
Isaias Miranda Viramontes*
Ana Luisa Gómez Blancarte**
Wilmer Hilmar Pérez Jiménez***
Con base en los conceptos de competencia y experiencia de significado de la teoría de comunidades de práctica, se analiza el proceso de toma de decisiones de un profesor universitario de matemáticas, quien, en reuniones de academia, propone implementar una nueva estrategia de enseñanza. La metodología fue cualitativa, en su modalidad de estudio de caso. Los resultados indican que dicho proceso está influenciado por la interrelación entre reflexiones cotidianas del profesor y las exigencias de su institución educativa. Se concluye que las distintas prácticas en las que el profesor participa en su labor profesional contribuyen en sus decisiones.
Palabras clave:
decisiones de profesores, profesores de matemáticas, teoría de comunidades de práctica, reuniones de academia
Based on the concepts of competence and experience of meaning of the theory of Communities of Practice, we analyze the decision-making process of a university mathematics professor who, in academy meetings, proposes to implement a new teaching strategy. The methodology was qualitative, in the form of a case study. The results indicate that this process is influenced by the interrelation between the professor's daily reflections and the demands of his educational institution. We conclude that the different practices in which the teacher participates in his professional practice contribute to his decisions.
Keywords:
teachers’ decision, mathematics teachers, Theory of Communities of Practice, academy meetings
Recibido: 21 de febrero de 2024 | Aceptado para su publicación: 10 de septiembre de 2024 |
Publicado: 16 de octubre de 2024
Cómo citar: Miranda Viramontes, I., Gómez Blancarte, A. L. y Pérez Jiménez, W. H. (2024). Decisiones en reuniones de academia: el caso de un profesor de matemáticas. Sinéctica, Revista Electrónica de Educación, (63), e1664. https://doi.org/10.31391/S2007-7033(2024)0063-012
* Doctor en Ciencias con especialidad en Matemática Educativa. Profesor-investigador del Programa de Matemática Educativa del CICATA-Legaria del Instituto Politécnico Nacional. Miembro del Sistema Nacional de Investigadores, nivel 1. Líneas de investigación: construcción social del conocimiento matemático y Estudios sobre la práctica docente y cultura matemática del profesor de matemáticas. Correo electrónico: imirandav@ipn.mx/https://orcid.org/0000-0003-2076-7383
* Doctora en Ciencias con especialidad en Matemática Educativa. Profesora-investigadora del Programa de Matemática Educativa del CICATA-Legaria del Instituto Politécnico Nacional. Miembro del Sistema Nacional de Investigadores, nivel 1. Líneas de investigación: desarrollo profesional docente del profesor de matemáticas y didáctica de la estadística y probabilidad. Correo electrónico: algomezb@ipn.mx/https://orcid.org/0000-0002-8837-8643
* Maestro en Ciencias en Matemática Educativa. Profesor de matemáticas en la Unidad Profesional Interdisciplinaria de Ingeniería, Campus Guanajuato, del Instituto Politécnico Nacional. Líneas de investigación: prácticas del profesor de nivel superior. Correo electrónico: wperez@ipn.mx/https://orcid.org/0009-0005-7055-0424

Introducción
A partir de los trabajos iniciales de Bishop (1976), Shavelson (1973) y Shulman y Elstein (1975) sobre los procesos de toma de decisiones de los profesores (ver también Borko et al., 2008), algunos educadores matemáticos han analizado los factores que influyen en las decisiones tomadas por los profesores durante sus prácticas de enseñanza (Pinzón y Gómez, 2019, 2021) y sus planificaciones de clase (Trouche et al., 2018). Otros han utilizado perspectivas cognitivas para estudiar cómo las creencias de los profesores respecto a la estructura de las matemáticas, sus conocimientos matemáticos y sus objetivos pedagógicos estimulan las decisiones de los profesores (por ejemplo, Schoenfeld, 2011; Stockero y Van Zoest, 2013).
Si bien las perspectivas cognitivas han contribuido a nuestro conocimiento de las decisiones de los profesores de matemáticas, Potari y Stouraitis (2019) reconocen que esas perspectivas tienen limitaciones y desventajas al momento de determinar los factores que subyacen a esas decisiones. Estas restricciones reflejan el hecho de que los marcos teóricos cognitivos “se centran en las decisiones de los profesores como algo que ocurre en sus mentes, en el flujo de la enseñanza” (p. 312). Asimismo, Potari y Stouraitis destacan que los investigadores que utilizan perspectivas cognitivas para analizar datos no profundizan en las razones por las que las decisiones de los profesores cambian regularmente, aunque mantengan las mismas creencias, objetivos y conocimientos matemáticos.
Dado que la enseñanza requiere que los profesores tomen continuamente decisiones (Sullivan y Mousley, 2001), otros autores han considerado que el estudio del complejo proceso de toma de decisiones puede realizarse con el uso de perspectivas sociales y socioculturales. Ambas perspectivas sostienen que los contextos sociales e institucionales contribuyen a moldear las decisiones de los profesores (Lande y Mesa, 2016). Potari y Stouraitis (2019), por ejemplo, aplicaron la teoría de la actividad histórico-cultural de Engeström (1999, 2001) para comprender las decisiones de tres profesores de matemáticas al enfrentarse a un nuevo plan de estudios de matemáticas. Estos autores encontraron que las decisiones de esos tres profesores estuvieron influenciadas por su reconocimiento de las contradicciones entre las exigencias del nuevo currículo y su voluntad de resolverlas. En un estudio anterior, Stouraitis et al. (2017) utilizaron la teoría de Engeström para especificar las tensiones y los conflictos que esos tres profesores experimentaron al introducir los nuevos materiales curriculares en sus aulas.
Si la práctica docente es la acción que debe estudiarse, Olson (1992) sugiere que ese estudio debería considerar las intenciones de los profesores para llevar a cabo dichas prácticas. Algunos estudios que reconocen la complejidad y riqueza de las prácticas laborales (por ejemplo, Contu y Willmot, 2006; Orr, 1996) apoyan la sugerencia de Olson según la cual el papel de los profesores de matemáticas no se limita a la práctica de enseñanza. Para tener una mejor comprensión de la práctica, es necesario tomar en cuenta cómo los profesores y sus prácticas se relacionan con las estructuras sociales en las que ellos se sitúan (Morgan, 2014).
Una forma de entender por qué los profesores toman decisiones diferentes en circunstancias similares consiste en observar la variedad de prácticas en las que están involucrados. Un ejemplo es el estudio de Skott (2013). Con base en la teoría social de comunidades de práctica (TCP) (Wenger, 2001), Skott propuso un marco para estudiar el papel de un profesor de matemáticas de secundaria en términos de su participación en diversas prácticas.
Tomando en cuenta las diversas prácticas a las que los profesores de matemáticas pertenecen dentro de una institución educativa, este artículo contribuye a explicar el proceso de toma de decisiones a partir del uso de una perspectiva social. Utilizamos los conceptos de experiencia de significado y competencia de la TCP (inicialmente propuestos para analizar el aprendizaje de los miembros de una comunidad de práctica) para examinar las decisiones de Víctor, un profesor universitario de matemáticas. El escenario en el que analizamos estas decisiones fue una serie de reuniones de academia que tuvieron lugar antes del comienzo de un semestre. Las reuniones fueron organizadas por la facultad a la que pertenece Víctor. La pregunta que guio la investigación fue: ¿cómo influyen la competencia y la experiencia de significado en el proceso de toma de decisiones de Víctor al momento de proponer a sus colegas una nueva forma de impartir un curso?
Marco teórico
Reuniones de academia: una práctica de la comunidad de profesores
Según Wenger (2001), la práctica es una práctica social que alude a lo que los individuos hacen en contextos históricos y sociales. La TCP entrelaza los conceptos de práctica y comunidad, de tal manera que una comunidad de práctica llega a ser entendida como un concepto único que establece que la práctica siempre ocurre en una comunidad; de hecho, la práctica es la “fuente de coherencia de una comunidad” (Wenger, 2001, p. 105). En un estudio anterior, Miranda y Gómez-Blancarte (2018) argumentan que, durante su labor profesional, los profesores de matemáticas constituyen una comunidad de práctica. Aparte de la enseñanza, los profesores se involucran en tres prácticas (de capacitación, de gestión y de academia) que dan forma a lo que hacen en su comunidad (véase figura).
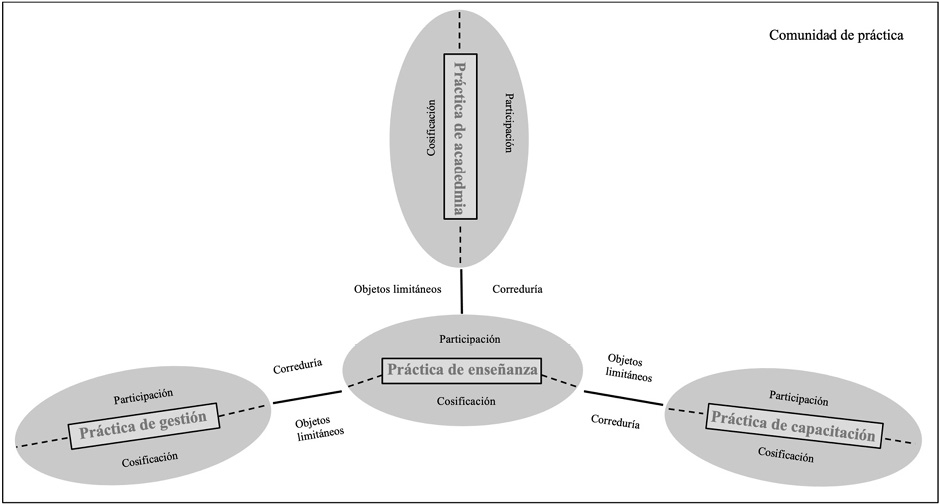
Figura. Relación entre las prácticas de los profesores. Fuente: Adaptado de Miranda y Gómez-Blancarte (2018).
Las tres prácticas institucionales mencionadas en la figura 1 son importantes porque influyen en el modo en que los profesores se comportan en clase (Miranda y Gómez-Blancarte, 2018). Las líneas sólidas indican que lo que los profesores hacen en su práctica docente impacta en las otras prácticas institucionales, y viceversa. Por ejemplo, cada profesor de matemáticas pertenece a una academia de matemáticas cuya orientación principal (“un patrón típico de actividades y conexiones a través del cual los miembros experimentan ser una comunidad” [Wenger et al., 2010, p. 258]) consiste en la celebración de reuniones en las que los profesores toman decisiones sobre temas como las dificultades de aprendizaje de los alumnos, las mejores estrategias didácticas para la enseñanza de contenidos específicos y asuntos disciplinarios.
Al situar la práctica de enseñanza como parte de una estructura educativa, las decisiones que los profesores toman están conectadas con las tomadas en las demás prácticas institucionales. Estas prácticas se influyen mutuamente a través de dos tipos de conexiones: objetos limitáneos (Star, 1989) y correduría (Wenger, 2001). Los objetos limitáneos actúan como un procesamiento de información; incluyen formas cosificadas de información como documentos y conceptos que los profesores aplican en una de estas prácticas, aunque se originen en otra.
La correduría, por su parte, se caracteriza como la participación necesaria para coordinar los significados de los objetos limitáneos y, a la vez, permitir la creación de nuevos significados (Wenger, 2001). En Miranda y Gómez-Blancarte (2018) se argumenta que los profesores actúan como corredores, pues crean conexiones entre las prácticas a las que pertenecen. Su experiencia de multiafiliación y la competencia que tienen en cada práctica explican las decisiones que toman dentro de cada práctica.
Competencia y experiencia de significado en el proceso de toma de decisiones
Al igual que la práctica, la competencia y la experiencia de significado son inseparables del concepto de comunidad de práctica. Según Wenger (2001), la competencia significa algo más que la capacidad de un individuo para realizar determinadas acciones (por ejemplo, enseñar, asistir a reuniones de la academia), poseer información o dominar ciertas habilidades. La competencia como miembro de una comunidad de práctica reside en desarrollar la capacidad de 1) crear relaciones en las que el compromiso mutuo sea la base de toda participación (por ejemplo, el compromiso para mejorar la enseñanza y el aprendizaje de las matemáticas); 2) contribuir a la comunidad comprendiendo su orientación principal (por ejemplo, proponer mejoras para la enseñanza); 3) utilizar el repertorio de todos los miembros de la comunidad para que la práctica sea más significativa (por ejemplo, reconocer las producciones de la academia y adoptarlas en la práctica). En otras palabras, la competencia es producida por la experiencia de la participación dentro y fuera de la comunidad, pero presupone la alineación con las normas establecidas dentro de esa comunidad. En este sentido, los profesores de matemáticas manifiestan su competencia al involucrarse en las prácticas de su comunidad educativa.
La experiencia de significado no solo se refiere a la comprensión pasiva de los objetos físicos o a la participación entusiasta en eventos que conducen a la acumulación de conocimientos, sino que también abarca lo que los individuos hacen realmente en la práctica (Wenger, 2001). En este caso, la práctica se convierte en el escenario en el que los miembros de una comunidad experimentan el significado de sus acciones. Al contribuir al desarrollo de la comunidad de práctica, los miembros se implican en las actividades a través de dos procesos: la participación y la cosificación (ver óvalos en la figura); es decir, es a través de los procesos de formar parte de la práctica y de producción de objetos que los profesores adquieren una experiencia de significado de su práctica. Como señalan Bohl y Van Zoest (2003), el conocimiento del individuo obtenido de la experiencia está relacionado con su propia competencia.
Método
La metodología del estudio fue cualitativa y de tipo documental, en su modalidad estudio de caso. Como señalan Cohen et al. (2007), este enfoque metodológico “puede captar la situación dinámica en el momento de la escritura” (p. 201). Dado que los mensajes de WhatsApp y de correo electrónico se escribieron en directo e in situ, pudimos captar parte del proceso de toma de decisiones de uno de los profesores. Este tipo de datos (mensajes y documentos) ha demostrado ser muy útil para realizar investigaciones educativas (por ejemplo, Stouraitis et al., 2017) e históricas (por ejemplo, Long, 2017).
Víctor y el contexto de su academia
El estudio se realizó en una universidad pública de México. La institución ofrece los siguientes cinco programas de ingeniería: Sistemas Automotrices, Aeronáutica, Biotecnológica, Farmacéutica e Industrial. La mayoría de los programas requieren varios de los mismos cursos de matemáticas, pero no necesariamente se imparten en el mismo semestre (la universidad tiene un sistema semestral; todos los programas constan de ocho semestres). Por ejemplo, el curso de Métodos numéricos (MN) se imparte en el cuarto semestre en todos los programas, excepto en Sistemas automotrices (en el que se imparte durante el segundo semestre) y Aeronáutica (en el que se imparte en tercer semestre). Ocho grupos de estudiantes de ingeniería estaban cursando la asignatura de MN en el momento de iniciar el estudio.
Este escenario nos condujo a realizar la investigación en un grupo de nueve profesores (dos mujeres y siete hombres) que impartían el curso de MN. El reglamento de la universidad estipula que todos los profesores que imparten el mismo curso organizan una academia; así, los nueve profesores formaron la Academia de Métodos Numéricos (AMN). Estos nueve profesores pertenecen al Departamento de Matemáticas (DM) de la universidad. El DM tiene un total de 18 profesores y tantas academias como cursos de matemáticas (por ejemplo, academia de Cálculo); así, los profesores pertenecían a más de una academia.
Los miembros de cada academia mantienen reuniones periódicas para discutir temas relacionados con la organización del curso (contenidos, número de exámenes parciales por semestre, etcétera). Todos los profesores del DM asisten, además, a un mínimo de tres reuniones de departamento cada semestre. Los acuerdos alcanzados en las reuniones de academia deben ser coherentes con los establecidos por el DM. La recopilación de datos para este estudio comenzó justo antes del inicio del segundo semestre del curso escolar, cuyo periodo comprendía de enero a junio de 2018.
La formación universitaria de los nueve profesores era diversa (en México, no todos los profesores universitarios tienen un diploma de doctorado): dos estudiaron física (uno con doctorado; otro, con maestría); siete estudiaron matemáticas (uno con doctorado; tres con maestría). En promedio, los nueve profesores tenían nueve años trabajando en la enseñanza. Algunos trabajaron como profesores de nivel básico antes de ser contratados por la universidad. Otros tenían más de cinco años en el DM, pero no necesariamente habían enseñado MN. Otros tenían menos de un año como profesores de MN.
Víctor era el único profesor que tenía el mismo tiempo de enseñar MN y de pertenecer al DM (ocho años) al momento de realizar esta investigación. Debido a esta característica, él fue el sujeto principal de nuestra investigación. Además de ser el profesor con más años enseñando MN, Víctor comenzaba el segundo año de sus estudios doctorales en Educación Matemática. De este modo, él estaba involucrado en tres prácticas: academia, capacitación y enseñanza.
El reglamento de la universidad estipula que todas las academias deben nombrar: un profesor titular y un profesor ayudante de cada curso; y un profesor que funja como jefe de la academia. Normalmente, los jefes son elegidos por los profesores miembros de la academia. Los miembros de la AMN eligieron a Víctor como jefe.
Es importante mencionar que, al realizar esta investigación, los miembros de la AMN habían propuesto tres cambios en la forma de enseñar. Durante los primeros cuatro años, los profesores impartían sus clases únicamente en sesiones presenciales y sin recursos audiovisuales. Los alumnos debían resolver ejercicios durante y fuera de la clase. La labor del profesor ayudante era responder a sus preguntas sobre el contenido de la clase y, cuando era necesario, ayudarles a resolver los problemas que el profesor titular les asignaba. En cada periodo de evaluación (tres por semestre), la calificación consistía en promediar las puntuaciones de los exámenes escritos y la puntuación total del conjunto de ejercicios de clase y trabajos asignados en casa.
Del quinto al octavo año, los profesores titulares impartieron las clases en sesiones presenciales y no presenciales. Víctor impartía sus clases en ambas modalidades. En cada periodo de evaluación, las calificaciones se basaban en el cálculo de la media de los resultados de los alumnos en un examen escrito (en línea o presencial) y la puntuación total en el conjunto de ejercicios de clase y trabajos asignados.
A principios del noveno año (enero de 2018), por sugerencia de Víctor, los profesores de MN modificaron su estrategia didáctica. Esta vez, la propuesta fue involucrar a los estudiantes en la estrategia didáctica denominada Recorridos de Estudio de Investigación (REI) (Chevallard, 2006), basada en el enfoque de la teoría antropológica de lo didáctico (Chevallard, 1999). La estrategia funciona mediante el desarrollo de actividades de investigación cuya característica principal es fomentar que los estudiantes se conviertan en investigadores. Esto se logra motivándolos a responder una pregunta generadora. Con este cambio, los profesores titulares de MN comenzaron a evaluar a los estudiantes al ponderar varios aspectos de su participación en las actividades de los REI.
Nuestro análisis se centra en las decisiones que Víctor tomó al comienzo del noveno año. El objetivo es explicar cómo llegó a proponer la incorporación de la estrategia REI en los planes de estudio de la AMN durante, y por medio de, su interacción con sus colegas en las reuniones de la AMN. La AMN no tenía reuniones programadas. Víctor, como jefe, avisaba a sus miembros las fechas de las reuniones, o bien, por medio del grupo de WhatsApp que él había organizado, o por correo electrónico. Estas solían celebrarse al principio del semestre y antes de los exámenes parciales.
Recolección de los datos
La recolección de datos consistió en recopilar mensajes de WhatsApp y correos electrónicos, realizar entrevistas y leer las actas de las reuniones celebradas en el semestre de enero a junio (no se nos permitió grabar las sesiones de las reuniones). En este artículo, reportamos solo los datos generados al inicio de este semestre. Con el consentimiento de sus compañeros, y dado que Víctor era el jefe de academia, los datos se recogieron principalmente de los documentos que él proporcionó. Nos centramos en las actas de las primeras reuniones tanto de la AMN como del DM y en los mensajes de WhatsApp y correo electrónico que Víctor envió antes de esas reuniones. También, solicitamos acceso a todos los mensajes de WhatsApp enviados a todos los miembros. Por último, mantuvimos entrevistas ocasionales (cara a cara o a distancia) con Víctor para aclarar temas de las actas de las reuniones de academia o de los mensajes de WhatsApp y de correo electrónico.
Para situar las decisiones de Víctor, y así comprender mejor el significado de las actas de las reuniones de academia y los mensajes electrónicos de él, revisamos dos documentos institucionales: las políticas y criterios de evaluación del DM y el reglamento académico de la universidad. El primero contiene, principalmente, todos los acuerdos tomados por el DM, la forma en que los profesores evalúan a sus alumnos, las directrices para asesorar a los estudiantes y los detalles del proceso de aplicación de exámenes parciales (escritos, orales, individuales). El segundo contiene las directrices para la creación de academias; además, especifica sus principales objetivos educativos. Según este último documento, las academias son órganos de representación cuyos objetivos principales consisten en analizar, evaluar y modificar los procesos educativos de la institución. Como se muestra en la siguiente sección, las propuestas de Víctor no podían llevarse a cabo sin el consentimiento de los demás profesores de la AMN.
Resultados
Identificamos dos temáticas relacionadas con las decisiones de Víctor: las estrategias didácticas y los procedimientos de evaluación. En este artículo, restringimos el análisis a la primera de ellas. Definimos las decisiones sobre estrategias didácticas como aquellas que, por un lado, inciden en la forma en que los profesores decidieron enseñar conceptos matemáticos específicos y, por otro, influyen en la modificación del contenido temático del plan de estudios. Con base en esta definición, encontramos que la AMN llegó a tres acuerdos: adoptar la modalidad de la estrategia REI en sus clases; flexibilizar los contenidos; y dividir el curso MN en dos fases. A continuación, analizamos el proceso de toma de decisiones de Víctor respecto a cada uno de estos acuerdos.
Propuesta de la estrategia REI
A principios del segundo semestre de enero-junio, mientras reflexionaba sobre los datos que había recogido para su tesis doctoral, Víctor envió un correo electrónico de cuatro párrafos a su asesora de tesis. En él, Víctor explicaba su intención de realizar una clase experimental con los alumnos que iban a cursar MN. El primer párrafo decía:
Para el siguiente semestre quisiera realizar un experimento para lo cual debo apresurarme a diseñar la planeación didáctica. Tendré tres grupos de métodos numéricos de ingeniería en sistemas automotrices de segundo semestre. Son cursos de 100 horas al semestre aproximadamente, por lo que generalmente la planeación por contenidos resulta holgada. Aún así, existe la problemática de que hay muchos reprobados y muchos estudiantes que aprueban olvidan las técnicas “aprendidas” en el curso. Entonces, se espera que se pueda tener una mejora en la aprobación mediante una mejoría en el involucramiento de los estudiantes y que “recuerden” más el curso poniendo énfasis en las competencias y no tanto en los contenidos (correo electrónico 1 de Víctor, párrafo 1, 8 de enero de 2018, énfasis añadido).
Víctor utilizó su experiencia, adquirida como profesor del curso, para justificar su plan didáctico al afirmar que un elevado número de alumnos suspende el curso de MN y otros olvidan pronto los contenidos. Al decir que “existe la problemática de que hay muchos reprobados y muchos estudiantes que aprueban olvidan las técnicas ‘aprendidas’ en el curso”, Víctor no tiene que aportar pruebas de su justificación. Es un hecho que él y sus colegas son conscientes de su experiencia conjunta. Como profesores, tienen competencia para afirmar la problemática observada.
Basado en esta experiencia, que tiene un significado específico para la práctica docente, y en la necesidad de definir el tema de su tesis doctoral, Víctor propuso diseñar un nuevo “experimento” de enseñanza; él creía que este sería eficaz para abordar los problemas identificados. Ahora bien, la simple mención del alto índice de fracaso en el curso de MN no era suficiente para justificar la propuesta de una estrategia docente distinta. Víctor tenía que ser competente para hacer tal propuesta. Su competencia se manifiesta en su conocimiento del contenido temático de MN y en su compromiso con su propio trabajo profesional y con otros profesores de MN, quienes también deseaban reducir el número de alumnos que fracasan en el curso. Otra condición que refleja la competencia de Víctor es que él propuso diseñar un plan didáctico basado en su conocimiento de la estrategia REI. Este plan lo elaboró en el mismo correo electrónico a su asesora:
La propuesta inicial se basa en la idea de que con una estrategia basada en actividades de indagación (REIs), los estudiantes tengan mayor motivación y desarrollen competencias que puedan ser usadas en el futuro. Tentativamente, los alumnos trabajarían con datos de GPS (Global Poiscion System) de trayectorias de corredores que se pueden obtener con diversas apps de smartphones (correo electrónico 1 de Víctor, párrafo 2, 8 de enero de 2018).
En este extracto, Víctor demuestra su competencia a través de su familiaridad con la metodología de los REI. Obsérvese cómo, incluso, él propone un tema (“datos del Sistema de Posición Global de las trayectorias de los corredores”) que podría servir para modificar la enseñanza de MN. Utiliza su competencia para proponer una nueva estrategia didáctica a fin de reducir el alto índice de fracaso en la asignatura de MN y ayudar a los alumnos a aplicar los contenidos temáticos de esta en otras asignaturas. En ese mismo correo electrónico, más adelante, Víctor es más concreto en su propuesta:
Uno de los primeros pasos o cuestión derivadas sería la del cálculo de la velocidad, con lo que posiblemente tendrían que estudiar fórmulas de diferencias finitas. Se espera que también comparen con otras formas de derivar. Por ejemplo, que interpolen con splines cúbicos y luego deriven. Así, en un análisis a priori se podría ver que más de la tercera parte de los contenidos temáticos del curso podrían estar involucrados. Así es que se tendrían que buscar una o dos cuestiones generatrices más para “cubrir” los temas del curso, aunque no sea necesario (correo electrónico 1 de Víctor 1, párrafo 3, 8 de enero de 2018, énfasis añadido).
Aquí, la experiencia de Víctor como profesor de MN, su experiencia en el uso de la estrategia REI (adquirida a través de sus estudios doctorales), su compromiso con la mejora tanto de su práctica docente como del aprendizaje de sus estudiantes, y su deseo de contribuir a la consecución de los objetivos de la AMN se articulan para dar lugar a una importante decisión respecto a la enseñanza de MN. En otras palabras, la decisión de Víctor se basa en la experiencia de significado que él tiene sobre su práctica docente, demostrada por su conocimiento de las dificultades que tienen los alumnos de aprobar el curso, y en su competencia, reflejada en su conocimiento del contenido conceptual del curso MN (práctica de enseñanza) y en el reconocimiento de una estrategia que le ayudaría a atender esas dificultades. Esta estrategia la conoció en el desarrollo de su investigación doctoral (práctica de capacitación).
Dado que la propuesta de la aplicación del REI requeriría la participación de al menos dos profesores, Víctor tuvo que persuadir a sus colegas de la AMN para que modificaran sus propias clases y aplicaran los principios de este enfoque. En primer lugar, aprovechó su papel de jefe de la AMN para explicar a algunos profesores, en una reunión informal y de manera verbal, su propuesta de curso. No pudimos obtener una transcripción de esa conversación, pero en una entrevista cara a cara Víctor declaró que presentó los mismos argumentos que en el correo electrónico enviado a su asesora. También les informó que la propuesta le serviría a él para su tesis doctoral. Tras obtener su aprobación, envió el siguiente mensaje de WhatsApp a todos los profesores de la AMN:
Estimados profesores, ayer varios profesores platicamos sobre una propuesta para cambiar la planeación de los cursos de numérico […]. Quedamos de escribir una propuesta y presentarla en una reunión de academia el próximo viernes [viernes 12 de 2018] [la reunión se pospuso al viernes 19 de 2018]. Creo que hoy en la noche les podré enviar la liga de un primer borrador (mensaje 1 de WhatsApp de Víctor, 9 de enero de 2018).
Con su intención de modificar el curso de todos los profesores de MN, Víctor demostró su competencia para establecer relaciones con sus compañeros. Dichas relaciones estuvieron mediadas por el deseo mutuo de reducir el alto índice de fracaso de los estudiantes de MN. En otras palabras, Víctor demostró su competencia al darse cuenta de que no bastaba con aprovechar las relaciones amistosas con algunos profesores de MN para impulsar su propuesta didáctica, sino que tenía que establecer relaciones profesionales para hacerla comprensible. Además, confirmó su competencia al tomar la iniciativa de escribir un borrador de propuesta en el que podría cosificar (en el sentido de Wenger, 2001) sus intenciones didácticas.
El documento que Víctor elaboró se llamó “Propuesta de modificación de los cursos de métodos numéricos en los cuatro programas de ingeniería” (en adelante, documento propuesta). Víctor compartió este documento con sus colegas de MN antes de la reunión del DM y, después de algunos cambios, todos los profesores de la AMN lo firmaron. La propuesta del documento se incluyó en el orden del día de la reunión del DM, en la que fue ratificada por la mayoría de los miembros de este departamento. Esta fue la redacción del acuerdo 11 del acta de esa reunión:
Se propuso el cambio en la planeación didáctica de las unidades de aprendizaje de Análisis Numérico, Métodos Numéricos y Métodos Numéricos taller. Este cambio será enfocado en el estilo de aprendizaje de Recorridos de Estudio en Investigación (REI). Se procedió a hacer la votación para aprobar la nueva planeación didáctica quedando aprobada por 10 votos a favor, 0 en contra y 3 abstenciones [nota: 5 profesores del DM no asistieron a esa reunión] (acta de la primera reunión del DM, 19 de enero de 2018, p. 5).
Como la AMN incluía a profesores que enseñan en diferentes programas de ingeniería, la decisión de incorporar la estrategia REI en los cursos de MN requirió que se modificaran los planes didácticos de cuatro de los cinco programas. A través del acuerdo 11, la propuesta de Víctor de incorporar la estrategia REI en los cursos de MN dejó de ser una propuesta individual para convertirse en una decisión colectiva que fue presentada a las autoridades universitarias con el apoyo de toda la AMN. Esto revela que el documento propuesta evidenció la experiencia de significado de los nueve profesores de MN. Dicho de otra manera, al solicitar que el DM formalizara la modificación del plan didáctico de MN, los profesores de la AMN mostraron su competencia a través de una contribución diseñada para cumplir con uno de los principales objetivos estipulados en el reglamento académico de la universidad: modificar los procesos educativos.
Las primeras explicaciones de Víctor no quedaron escritas en el texto del acuerdo 11, pero en una entrevista informal posterior afirmó que las justificaciones que presentó al DM eran las mismas que había ofrecido a su asesora en sus correos electrónicos. La experiencia de numerosas calificaciones reprobatorias entre los estudiantes del curso de MN fue compartida no solo por los profesores de la AMN, sino también por la mayoría de los miembros del DM. En términos de Wenger (2001), el acuerdo 11 representa, por un lado, una cosificación del intento de los profesores de MN de disminuir la tasa de reprobación, y, por otro, un objeto limitáneo que podría permitirles conectar su práctica de academia con su práctica de enseñanza. Aún más, este acuerdo constituía un objeto limitáneo que conectaba la práctica de capacitación de Víctor con sus prácticas de academia y enseñanza. De hecho, en el momento en que los profesores de MN implementaron la estrategia REI, se convirtieron en corredores (Miranda y Gómez-Blancarte, 2018).
La decisión de implantar los cursos de MN con la estrategia REI también condujo a sustituir el contenido temático del curso anterior por nuevos temas, así como a introducir cierta flexibilidad en el contenido temático. En la siguiente sección se examina cómo se tomó esta decisión.
Temas de contenido flexibles
La decisión de incorporar la estrategia REI en los cursos de MN supuso la modificación del plan didáctico de cada profesor de MN y de todo el programa de estudios. Un análisis de las decisiones que subyacen en el documento propuesta, en términos de competencia y experiencia de significado de los profesores, puede dilucidar cómo fue posible esta modificación.
Además de destacar que MN tenía un alto índice de reprobación, los profesores dieron otras tres razones para apoyar la propuesta de aplicar la estrategia REI en su presentación al DM:
Inaplicabilidad en semestres posteriores. Frecuentemente los estudiantes solicitan asesorías para resolver problemas que se les presentan en otros cursos y no tienen la mínima idea cómo resolverlo. Cambiaría este punto por conocimientos no significativos. Los estudiantes recuerdan nombres de los métodos y cuentan con algunos programas para resolver problemas elementales, pero no ubican el contexto en el cual pueden aplicarse para resolver problemas de ingeniería.
Conocimientos no aplicados. Solamente se presentan aplicaciones en ejercicios simplistas.
Problemas aislados. A pesar de que ha habido esfuerzos de integrar la “Unidad de Aprendizaje” [se refiere al curso MN], pocos estudiantes logran ver las relaciones entre diferentes temas (documento propuesta, 9 de enero de 2018, p. 1).
En este caso, los profesores de MN describieron un problema recurrente en los cursos de matemáticas: el contenido de MN se presenta aislado a menudo. También reconocieron que, aparte de los problemas rutinarios que surgen durante las clases, los alumnos encuentran grandes dificultades cuando intentan aplicar sus aprendizajes para adquirir nuevos conocimientos. Para resolver estas problemáticas, la propuesta de los profesores tenía que apuntar en la dirección contraria; es decir, las modificaciones del programa de estudios de MN no podían consistir simplemente en la sustitución de ciertos temas o en el cambio del orden de su presentación, sino en garantizar la interconexión de todos los temas. Debido a las propiedades metodológicas de la estrategia REI, el documento propuesta sugería flexibilizar el contenido del curso. En este sentido, la decisión de utilizar la estrategia REI para mejorar la comprensión de los alumnos del contenido de MN condujo a cambios fundamentales en el programa de estudios. La competencia de Víctor para realizar estas modificaciones se observa en que él motivó a sus colegas a redefinir el programa de estudios de MN y a añadir nuevos repertorios (por ejemplo, el lenguaje común del significado de la estrategia REI).
Como parte de sus esfuerzos para justificar que esta estrategia es un enfoque que resuelve la problemática de abordar temas aislados en las aulas de MN, los profesores incluyeron, en el documento propuesta, una breve descripción de la estrategia REI y los antecedentes teóricos que la sustentan:
Los REIs se generan a partir de una cuestión generatriz que los estudiantes tratan de responder con la ayuda de los profesores. Estos dispositivos didácticos están en armonía con la técnica de Aprendizaje Basado en Problemas (ABPs). En los REIs no necesariamente se parte de un escenario, aunque puede ser que sí. Los REIs se concibieron dentro de una teoría con la cual se pueden hacer análisis didácticos. Tanto ABPs como REIs pertenecen a una familia más amplia de estrategias didácticas que se pueden nombrar como Aprendizaje Basado en la Indagación (Inquiry Based Learning) a la que también pertenecen Resolución de Problemas (Problem Solving) y Educación en Matemáticas Realistas (Realistic Mathematics Education) (documento propuesta, 9 de enero de 2018, pp. 1-2).
Aunque esta explicación fue mencionada por Víctor, el hecho de que fuera redactada en un documento oficial firmado por los miembros de la AMN significa que todos ellos habían estado de acuerdo con ella. A pesar de que Víctor era el único miembro que conocía en profundidad el enfoque de los REI, la explicación tomó en cuenta la experiencia compartida de los profesores de MN (porque justifica una manera de atender el aislamiento de los temas) y la competencia de Víctor, quien sabía de antemano que la aplicación de esta estrategia requeriría la modificación de cuatro programas de ingeniería.
De hecho, dada la diversidad de temas que se abordan en los cursos de MN de cada uno de los cuatro programas de ingeniería (Industrial, Sistemas Automotrices, Biotecnología y Farmacéutica), la estrategia REI permite abordar esta diversidad sin un orden estricto de presentación. En su documento propuesta, los profesores de MN dieron a entender que el programa de estudios de MN de cada programa impide a los estudiantes identificar los contextos en los que los conocimientos adquiridos podrían aplicarse. Así, ellos argumentaron que este obstáculo puede superarse al usar la estrategia REI.
A su vez, los profesores de MN esbozaron un primer proyecto relacionado con dos actividades de investigación, implicadas en la estrategia REI. Afirmaron que varios temas podrían incluirse en el programa de estudios de cada programa de ingeniería sin estipular un orden determinado de presentación. Basándose en esta estrategia, incluyeron una sección denominada “Consideraciones iniciales del curso”, en la que propusieron la siguiente pregunta generadora: “¿Cómo se puede analizar el rendimiento de un corredor si se cuenta con sus registros de GPS?” (documento propuesta, p. 2). Esta pregunta fue el principal mecanismo a través del cual los profesores decidieron modificar el programa de estudios de MN y hacerlo más flexible. En el documento propuesta que presentaron al DM afirmaron que una de las funciones de la pregunta generadora es estimular a los estudiantes a crear preguntas como: “¿Cuál es la distancia entre dos puntos cuyas coordenadas terrestres están dadas?” (documento propuesta, p. 2). Los profesores, incluso, narraron un posible escenario en el que los estudiantes podrían responder a esta pregunta: afirmaron que los estudiantes pueden “encontrar los puntos [del corredor] en Google Maps y pedirle [a Google Maps] que encuentre [la distancia]” (documento propuesta, p. 3).
La decisión de incluir estas dos preguntas generadoras explícitamente en el documento propuesta demostró la competencia de los profesores de MN al proporcionar una comprensión más clara de lo que querían decir al conectar entre sí los temas de los diferentes cursos de MN. En términos de la teoría de Wenger (2001), las dos preguntas generadoras (¿cómo se puede analizar el rendimiento de un corredor si se cuenta con sus registros de GPS? y ¿cuál es la distancia entre dos puntos cuyas coordenadas terrestres están dadas?), en particular, y el documento propuesta, en general, son cosificaciones de la decisión de los profesores de implementar una nueva forma de enseñar MN. De hecho, el documento propuesta es un objeto limitáneo que conecta la práctica de academia de los profesores con su práctica de enseñanza.
El documento propuesta puede entenderse como una decisión colectiva basada en la competencia de Víctor para comprender las ventajas de la estrategia REI, así como en su experiencia de significado al asentir que los planes de estudio de MN de los cuatro programas de ingeniería presentaban temas no relacionados unos con otros. En otras palabras, el documento propuesta fue una decisión cosificada que fusionó la competencia de Víctor con su experiencia de significar su trabajo docente.
Además de flexibilizar el plan de estudios, la AMN tomó otra decisión, causada por la incorporación de la estrategia REI. Dicha decisión consistió en dividir el curso en dos proyectos.
Dividir el curso de MN en dos proyectos
Una vez que el DM escribió el acuerdo 11, los profesores de MN elaboraron un documento de cuatro páginas llamado “Guía del curso de métodos numéricos” (en adelante, guía), la cual ampliaba la información del documento propuesta, enumeraba los objetivos de aprendizaje y especificaba cómo los profesores evaluarían el aprendizaje de los estudiantes. También en ella se describía la metodología con la que los profesores proponían cubrir todos los temas de los diferentes programas de ingeniería por medio de persuadir a sus estudiantes a que respondieran las preguntas generadoras. La metodología consistía en involucrar a los alumnos en dos proyectos. El nombre del primer proyecto sería “Rutas GPS”, mientras que el segundo se llamaría, simplemente, “Aún por nombrar” (en la guía, los profesores especificaron que este segundo proyecto se entregaría antes de implementar el segundo examen parcial).
Es importante señalar que el origen de la decisión de llamar “Rutas GPS” al primer proyecto se encuentra en el párrafo 2 del correo electrónico de Víctor a su directora de tesis. En él, Víctor indicó que el nombre “Rutas GPS” no era una decisión espontánea, tomada por la AMN. A continuación, se muestra este párrafo:
Para el análisis [de los datos del GPS], [los estudiantes] podrían usar un software matemático de su elección, pero que fuera accesible y legal para el resto de los participantes (por ejemplo, Geogebra, Scilab, wxMaxima, R, Excel, Octave, etc.). La cuestión [pregunta] generatriz aún no está definida, pero podría estar relacionada con una preparación para la carrera [se refiere a un maratón organizado por la universidad] (correo electrónico 1 de Víctor, párrafo 2 (continuación), 8 de enero de 2018, énfasis añadido).
Este texto muestra que Víctor había previsto las características de la pregunta generatriz antes de la primera reunión del DM. De esta forma, el proyecto 1 cosificó una intención didáctica que Víctor había concebido antes de presentarla a la consideración de sus colegas, pero Víctor hizo también otra cosificación. En su segundo correo electrónico a su asesora, él responde una pregunta que ella le escribió en relación con los motivos de incluir datos del GPS en su propuesta:
Con respecto a la pregunta de que lleva a producir la cuestión generatriz, en este caso, es “mi experiencia personal”. Los datos de GPS los uso para entrenar. De pronto, deseaba obtener información que ya no brindaban los informes de las apps. Por ejemplo, algunas apps te dicen cuál fue tu kilómetro más rápido en una carrera de 5 kms. Pero, ¿qué podía hacer si yo deseaba los 800s más rápidos? De ahí surgió la idea, aunque la cuestión generatriz se trató de adaptar a las condiciones escolares (correo electrónico 2 de Víctor, párrafo 1, 12 de enero de 2018, énfasis añadido).
Así, el proyecto 1 y la pregunta generatriz cosificaron no solo las intenciones didácticas de Víctor, sino también su experiencia personal como corredor y la forma en que participó en la práctica de la AMN. Más concretamente, las experiencias de hacer ejercicio y de intentar medir su esfuerzo (“¿qué podía hacer si yo deseaba los 800s más rápidos?”) le proporcionaron un significado didáctico que podía implementarse en su práctica docente. Al reflexionar sobre cómo su experiencia personal como corredor podía utilizarse en su trabajo profesional, Víctor aportó a su práctica de academia nueva información que ayudaría a los miembros a tomar decisiones sobre su propia práctica de enseñanza. El proyecto 1 conecta, por así decirlo, las habilidades atléticas de Víctor con sus habilidades docentes, pero también es el resultado de que Víctor exprese (verbalmente y por escrito) y negocie sus intenciones didácticas con sus colegas. Para lograrlo, necesitaba comunicar su experiencia como atleta y convencer a sus colegas de que podía utilizarse con fines didácticos. Estas acciones (comunicar y convencer) forman parte del proceso de participación de Víctor dentro de esta comunidad de profesores de MN.
Analizada en retrospectiva, reiteramos que la decisión de poner en marcha los dos proyectos formó parte de una cadena de decisiones caracterizada por una relación entre la competencia de Víctor y su experiencia de significado. En este sentido, los dos proyectos cosificaron el proceso de participación de Víctor en el que él se involucró durante las reuniones de academia. Aunque estos proyectos no fueron planificados inicialmente ni por Víctor ni por los profesores de la AMN, surgieron a partir de la necesidad de adaptar y adoptar los REI como estrategia de enseñanza. A su vez, la decisión de tener dos proyectos permitió que Víctor (y, a la vez, sus colegas) reconocieran la necesidad de dividir el curso en dos partes. Los dos proyectos son ejemplos de cómo las decisiones de Víctor, en el contexto fuera del aula de clases, pueden repercutir en la práctica de enseñanza y, por tanto, ejemplifican la conexión de la práctica de academia y la práctica de capacitación con la práctica de enseñanza (véase figura).
Conclusiones
En este artículo, centramos nuestra atención en el proceso de toma de decisiones de un profesor de matemáticas (Víctor) durante su interacción con sus colegas en reuniones de academia. Con base en la teoría del aprendizaje de Wenger (2001), sus decisiones fueron analizadas en términos de competencia y experiencia de significado. Estos conceptos fueron utilizados inicialmente por Wenger para conceptualizar el aprendizaje; sin embargo, nuestra propuesta teórica consistió en aplicarlos al estudio de las decisiones.
A partir de nuestra interpretación de los mensajes de WhatsApp y de correo electrónico, de los documentos institucionales y de las entrevistas personales, afirmamos que las tres decisiones (propuesta de la estrategia REI, flexibilizar los contenidos y dividir el curso MN en dos proyectos) fueron, de alguna manera, resultado de la experiencia personal y docente de Víctor y de su capacidad para crear un nuevo compromiso mutuo con sus colegas para impartir un curso de matemáticas. Aunque la experiencia del significado y la competencia son más explícitas en el caso de Víctor, es importante señalar que sus colegas contribuyeron con su experiencia y competencia para que las propuestas de Víctor fueran aceptadas. Por un lado, sus colegas compartían la experiencia de las dificultades de los alumnos para comprender los contenidos del curso de MN. Por otro, el hecho de que sus colegas se comprometieran a aplicar la estrategia REI revela un acto de competencia, pues pudieron contribuir a una mejor comprensión de esta estrategia y así aplicarla en su curso de MN.
Nuestro estudio intentó destacar el hallazgo de que las decisiones de un profesor, tomadas fuera del entorno del aula, son importantes para mejorar la práctica de enseñanza. Aunque las decisiones tomadas por los profesores en contextos momentáneos durante su práctica docente están directamente relacionadas con lo que los estudiantes aprenden (o no), el análisis de las decisiones de Víctor muestra que lo que él decidió dentro de su práctica de academia puede cambiar la forma en que se produce el aprendizaje de los estudiantes. De hecho, la práctica de academia y, más precisamente, las reuniones de academia son escenarios que pueden estar asociados a lo que Herbers et al. (2011) identificaron como el territorio “en el que los profesores deciden lo que vale la pena aprender, la naturaleza y la secuencia de las actividades de enseñanza, así como lo que es el éxito y el fracaso” (p. 105).
El proceso de decisión de lo que vale la pena aprender es lo que nuestro estudio se propuso dilucidar. Creemos que nuestra investigación concuerda con el enfoque documental de la didáctica de Trouche et al. (2018), en el sentido de que el análisis de las sesiones de planificación docente ayuda a comprender las acciones de los profesores en el aula.
Sin embargo, también creemos que examinar las decisiones de los profesores a través de los conceptos derivados de la TCP nos permite estudiar cómo aprenden a enseñar. En otras palabras, las decisiones de los profesores pueden ser herramientas metodológicas para estudiar sus propios procesos de aprendizaje. En este caso, el proceso de aprendizaje no consiste en la comprensión de conceptos matemáticos concretos, sino en la actuación docente. El profesor entra en el escenario del aula, por así decirlo, y actúa de una manera determinada, pero tras bambalinas tiene lugar una gran cantidad de actividad. Como señalan Kim et al. (2020), la planificación de una lección puede ser el lugar donde los profesores aprenden.
Volviendo a nuestro estudio, el análisis de las decisiones de Víctor muestra que, durante los procesos de toma de decisiones fuera del aula, los profesores pueden crear condiciones en las que podrían mejorar su proceso de toma de decisiones dentro del aula; es decir, los profesores pueden aprender a través de sus decisiones. También, revela que el aprendizaje de los profesores puede ser explorado a través de su proceso de participación en el desarrollo de la práctica de academia. Dicho de otro modo, lo que hacen los profesores universitarios en su práctica de academia constituye el aprendizaje, y lo que aprenden es su práctica de enseñanza. En términos más generales, aprenden mediante la participación y cosificación de su práctica (Gómez-Blancarte y Miranda, 2021). El acto de enseñar no puede, por tanto, reducirse a un conjunto de habilidades didácticas que los profesores deben adquirir, sino que puede percibirse como parte de una cadena de decisiones que ellos toman durante su interacción con los miembros de su comunidad de práctica. En general, los profesores entran en el aula con un aprendizaje que han adquirido colectivamente.
Esta afirmación está en consonancia tanto con los hallazgos de Mercado-Maldonado (2002), relacionados con la forma en que las diversas experiencias fuera del aula influyen en la práctica docente de los maestros de preescolar, como con lo que señalan D’Eon et al. (2000): “El rendimiento de un profesor mejoraría no solo por haber aprendido una nueva estrategia, sino como resultado de su examen crítico y colegiado y de la comprensión de una gama más amplia de normas que influyen en lo que hace en el aula” (p. 160).
Una de las implicaciones de esta investigación se refiere a la importancia de otras prácticas institucionales en las que los profesores participan necesariamente durante su labor profesional en relación con su propio aprendizaje. Las tres prácticas (capacitación, de academia y de enseñanza) en las que participó Víctor son ejemplos de prácticas institucionales por medio de las cuales se produce el aprendizaje de los profesores. Al participar en distintas prácticas, como lo hizo Víctor, los profesores son capaces de cosificar lo que hacen en esas prácticas para aprender a enseñar (Miranda y Gómez-Blancarte, 2018).
A la luz de esta investigación, las instituciones educativas podrían considerar que las reuniones de academia pueden servir no solo para discutir asuntos administrativos, sino también para fomentar el aprendizaje de los profesores como resultado de los acuerdos que sus profesores puedan alcanzar. Una posible forma de continuar investigando sobre la influencia de las instituciones educativas en el aprendizaje de los profesores consiste en desarrollar un estudio longitudinal que examine, por un lado, cómo las decisiones de los miembros de una academia se implementan en el aula y, por otro, cómo esas decisiones impactan en la mejora del aprendizaje de conceptos matemáticos por parte de los estudiantes.
Referencias bibliográficas
Bishop, A. J. (1976). Decision-making, the intervening variable. Educational Studies in Mathematics, vol. 7, núm. 1–2, pp. 41–47. https://doi.org/10.1007/bf00144357
Bohl, J. V. y Van Zoest, L. R. (2003). The value of Wenger’s concepts of modes of participation and regimes of accountability in understanding teacher learning. En N. A. Pateman, B. J. Dougherty, y J. T. Zilliox (eds.). Proceedings of the 27th Conference of the International Group for the Psychology of Mathematics Education held jointly with the 25th Conference of PME-NA (pp. 339–346). Center for Research and Development Group.
Borko, H., Roberts, S. A. y Shavelson, R. (2008). Teachers’ decision making from Alan J. Bishop to today. En P. Clarkson y N. Presmeg (eds.). Critical Issues in Mathematics Education (pp. 37–67). Springer. https://doi.org/10.1007/978-0-387-09673-5_4
Chevallard, Y. (2006). Steps towards a new epistemology in mathematics education. En M. Bosch (ed.). Proceedings of the 4th Conference of the European Society for Research in Mathematics Education (pp. 21–30). Universidad Ramon Llull. http://erme.site/wp-content/uploads/2021/06/CERME4_2_Plenaries.pdf
Chevallard, Y. (1999). L’analyse des pratiques enseignantes en théorie anthropologique du didactique. Recherches en Didactique des Mathématiques, vol. 19, núm. 2, pp. 221–266. https://revue-rdm.com/1999/l-analyse-des-pratiques/
Cohen, L., Manion, L. y Morrison, K. (2007). Research methods in education. Routledge.
Contu, A. y Willmot, H. (2006). Studying practice: situating talking about machines. Organization Studies, vol. 27, núm. 12, pp. 1769–1782. https://doi.org/10.1177/0170840606071895
D’Eon, M., Overgaard, V. y Rutledge, H. S. (2000). Teaching as a social practice: Implications for faculty development. Advances in Health Sciences Education, vol. 5, núm. 2, pp. 151–162. http://doi.org/10.1023/A:1009898031033
Engeström, Y. (2001). Making expansive decisions: An activity-theoretical study of practitioners building collaborative medical care for children. En C. M. Allwood y M. Selart (eds.). Decision making: social and creative dimensions (pp. 281–301). Springer. https://doi.org/10.1007/978-94-015-9827-9_14
Engeström, Y. (1999). Activity theory and individual and social transformation. En Y. Engeström, R. Miettinen y R. L. Punamäki (eds.). Perspectives on activity theory (pp. 19–39). Cambridge University Press. https://doi.org/10.1017/CBO9780511812774
Gómez-Blancarte, A. L., y Miranda, I. (2021). Participation and reification: Two basic design principles for mathematics professional development programs. Canadian Journal of Science, Mathematics and Technology Education, vol. 21, núm. 3, pp. 625–638. https://doi.org/10.1007/s42330-021-00175-1
Herbers, M. S., Antelo, A., Etting, D. y Buck, A. M. (2011). Improving teaching through a community of practice. Journal of Transformative Education, vol. 9, núm. 2, pp. 89–108. https://doi.org/10.1177/1541344611430688
Kim, H.-j., Metzger, M. y Heaton, R. M. (2020). Teacher planning sessions as professional opportunities to learn: An elementary mathematics teacher’s re-conceptualization of instructional triangles. International Journal of Science and Mathematics Education, vol. 20, pp. 1207–1227. https://doi.org/10.1007/s10763-019-10019-y
Lande, E. y Mesa, V. (2016). Instructional decision making and agency of community college mathematics faculty. ZDM Mathematics Education, vol. 48, núm. 1–2, pp. 199–212. https://doi.org/10.1007/s11858-015-0736-x
Long, M. (2017). High medieval monasteries as communities of practice: approaching monastic learning through letters. Journal of Religious History, vol. 41, núm. 1, pp. 42–59. https://doi.org/10.1111/1467-9809.12345
Mercado-Maldonado, R. (2002). Los saberes docentes como construcción social. La enseñanza centrada en los niños. Fondo de Cultura Económica.
Miranda, I. y Gómez-Blancarte, A. L. (2018). La enseñanza de las matemáticas con el enfoque de la teoría de comunidades de práctica. Educación Matemática, vol. 30, núm. 3, pp. 269–288. https://doi.org/10.24844/em3003.11
Morgan, C. (2014). Understanding practices in mathematics education: structure and text. Educational Studies in Mathematics, vol. 87, núm. 2, pp. 129–143. https://doi.org/10.1007/s10649-013-9482-6
Olson, J. K. (1992). Understanding teaching. Beyond expertise. Open University Press.
Orr, J. E. (1996). Talking about machines: An ethnography of a modern job. Cornell University Press.
Pinzón, A. y Gómez, P. (2021). Toma de decisiones en el aula: estudio de casos de profesores de matemáticas. PNA, vol. 16, núm. 1, pp. 1–24. https://doi.org/10.30827/pna.v16i1.15674
Pinzón, A. y Gómez, P. (2019). Un modelo para la toma de decisiones del profesor de matemáticas. PNA, vol. 13, núm. 3, pp. 130–146. https://doi.org/10.30827/pna.v13i3.7908
Potari, D. y Stouraitis, K. (2019). Teacher decision making. En D. Potari y O. Chapman (eds.). International Handbook of Mathematics Teacher Education: Volume 1 (pp. 303–325). Brill. https://brill.com/display/title/60697
Schoenfeld, A. (2011). How we think. A theory of goal-oriented decision making and its educational applications. Routledge.
Shavelson, R. J. (1973). What is the basic teaching skill? Journal of Teacher Education, vol. 24, núm. 2, pp. 144–151. https://doi.org/10.1177/002248717302400213
Shulman, L. S. y Elstein, A. S. (1975). Studies of problem solving, judgment, and decision making: Implications for educational research. En F. N. Kerlinger (ed.). Review of Research in Education (pp. 3–42). F. E. Peacock. https://doi.org/10.2307/1167252
Skott, J. (2013). Understanding the role of the teacher in emerging classroom practices: searching for patterns of participation. ZDM Mathematics Education, vol. 45, núm. 4, pp. 547–559. https://doi.org/10.1007/s11858-013-0500-z
Star, S. L. (1989). The structure of ill-structured solutions: Boundary objects and heterogeneous distributed problem solving. En L. Gasser y M. N. Huhns (eds.). Distributed artificial intelligence (pp. 37–54). Ptman. https://doi.org/10.1016/B978-1-55860-092-8.50006-X
Stockero, S. y Van Zoest, L. (2013). Characterizing pivotal teaching moments in beginning mathematics teachers’ practice. Journal of Mathematics Teacher Education, vol. 16, núm. 2, pp. 125–147. https://doi.org/10.1007/s10857-012-9222-3
Stouraitis, K., Potari, D. y Skott, J. (2017). Contradictions, dialectical oppositions and shifts in teaching mathematics. Educational Studies in Mathematics, vol. 95, núm. 2, pp. 203–217. https://doi.org/10.1007/s10649-017-9749-4
Sullivan, P. y Mousley, J. (2001). Thinking teaching: Seeing mathematics teachers as active decision makers. En F. L. Lin y T. J. Cooney (eds.). Making sense of mathematics teacher education (pp. 147–163). Kluwer Academic Publishers. https://doi.org/10.1007/978-94-010-0828-0_7
Trouche, L. Gueudet, G. y Pepin, B. (2018). Documentation approach to didactics. En S. Lerman (ed.). Encyclopedia of Mathematics Education (pp. 1–11). Springer. https://doi.org/10.1007/978-3-319-77487-9_100011-1
Wenger, E. (2001). Comunidades de práctica: aprendizaje, significado e identidad (G. Sánchez Barberán, traducción). Paidós Ibérica.
Wenger, E., White, N. y Smith, J. (2010). Learning in communities. En U. D. Ehlers y D. Schneckenberg (eds.). Changing cultures in higher education. Moving ahead to future learning (pp. 257–284). Springer. https://doi.org/10.1007/978-3-642-03582-1_20